© Peter Broadfoot 2008
Histograms
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
Weight / kg
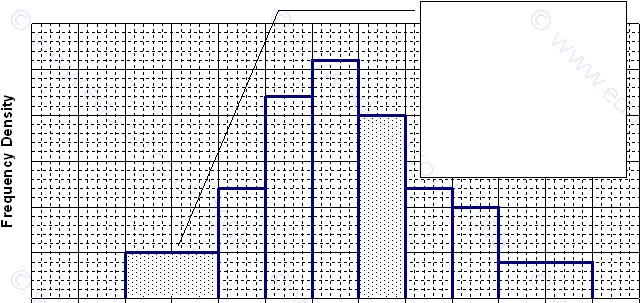
Calculate the number of data
items between 1 and 2kg, given
that there are 10 items in the 3.5
to 4kg box. Call the frequencies
of the two shaded areas fs for the
short box and ft for the tall box.
The ratio of the areas is 2:4 = 1:2
and so, fs/ft = 1/2 = ½ Therefore
fs = ½×ft = ½×10 = 5 items
Exam Questions on Frequency Density
It will be clear from the question if you are expected to use frequency density. It is almost
certain that a Higher tier question, that specifically mentions a histogram, will use
frequency density on the y-axis. If the bars (the classes) are the same width, the height of a
bar is proportional to the frequency it represents. In a typical question the bars are not all
the same width (see the sample exam question, next page). Then you use the areas of the
bars, not the heights, to compare the frequencies.
Usually the chart’s grid consists of 1cm squares. In the example below the histogram
shows the weights of items. The two shaded boxes are different widths. Count the 1cm
squares. The wide shaded box is 2 squares. The tall shaded box is 4 squares. You are told
that the number of items (the frequency) in the tall box, from 3.5 to 4kg, is 10. How many
items are in the wide box, between 1 and 2kg? Compare the areas. The tall box is twice the
area and therefore twice the frequency. The frequency for the smaller box is half of 10.
Write that as an equation: f = ½ × 10 = 5. The number is 5.
You may prefer a variation on the calculation. You can start by calculating the number of
items in one square. You know that there are 10 items in the 4 squares of the tall box
(f=10), and so calculate the number of items per 1cm square.
The number of items in 1 square = 10/4 = 2.5
Therefore, in a box with two squares, the number of items = 2×2.5 = 5
Exercise 5 – Reading a Histogram
For the histogram above, each 1cm square represents 2.5 items of data. Calculate the
number of items that weigh between 4.5 and 6kg.